Gálapagos Project Announcement
In this announcement we will officially kick off the main two endeavors of the project:
- The GoL combinatorial database construction
- The Gemini Expedition
In the following post we address a little bit the history of the project and present a brief overview of the main project components.
The Fundamental Observation
This project has four fundamental sources that come all the way back to the summer of 2020. These are:
The Combinatorial theory of evolution and economics
The Wolfram Physics Project
The Empirical theory of Metamathematics
The Game of Life(GoL) cellular automata
Each of them developed separately until April 12th, 2021, where I was able to develop a framework where they all fit together. This framework allowed me to see an unexplored territory and convinced me to start this project. Next, I’ll describe each source’s development briefly and the key insight that allowed me to unify all of them.
The Combinatorial Theory of Evolution and Economics
I’ve been thinking quite deeply about economics since summer 2020 when I started meeting weekly with my friend Andrés Gallegos, an Economist at the IDB(Inter-American Development Bank). Our plan was to study the possible relation between physics, economics, and information theory. We discussed resource theories, economic complexity, economic inequality, biology, evolutionary complexity, information value, innovation, and growth, among other things. Although we didn’t obtain any concrete result. I learned a lot from a top-level economist, and my interest in economics just got stronger.
Later that year while listening to the Complexity Podcast from the Santa Fe Institute, I encountered the episode W. Brian Arthur (Part 1) on The History of Complexity Economics. Of course, I listened to this episode due to my interests in economics and complexity. In this episode, Brian Arthur discusses how technology evolves, and a theory he developed called the Combinatorial Theory of Evolution. At the time the theory made a lot of sense to me: we combine pieces of technologies to generate more complicated technologies. In Brians’s own terms: “ It turns out this isn’t a terribly deep insight but nor was Darwin’s, but it was crucial.” The episode continued with how this theory relates to economics and other areas of knowledge. Something that particularly struck me was when he mentioned:
“And that would be that individual pieces or parts, whether this is in technology or indeed in parts of mathematics even. Think of things like theorems — new theorems are constructed by combining old ones with syntax and mathematical logic and grammar. To give new statements that might be proofs or conjectures even.” — W. Brian Arthur. Complexity Podcast.
This was an outlandish claim, surely mathematics is much more complicated than putting known machines together to form a new machine. This is just the inner workings of Lego. I didn’t believe this claim at the time. Nevertheless, it stuck in my mind.
The Wolfram Physics Project
In the summer of 2019, I got completely convinced that chapter 9 on Fundamental Physics of the New Kind of Science(NKS) contained breakthroughs that had not been explored in the scientific literature for about two decades. In that chapter Stephen Wolfram described how he derived General relativity with a series of trivalent graphs with a similar method to fluid cellular automation he described years earlier, but did not provide the details of this formulation. Since I had a mature understanding of these methods and computational methods for differential geometry, I thought that it was an incredible omission not to pursue these ideas further. Those days I put myself the objective to study for the next ten years to decipher what did he meant about those words, when the pandemic hit in march 2020 I was already studying the papers from Stephen on cellular automata when the announcement of a future physics project was on the cusp.
More than just the particular aspects of the Stephen proposal, I was deeply convinced that physics needed to deeply absorb the ideas of computation in order to progress to the 21st century. It is an absolute catastrophe that physicists today are still using paper and pencil to do their models. But seriously, more than doing physics on a computer, the fundamental question is: what fundamental aspects can computation give to physics? and reversely what can physics contribute to computation? Quite a bit of effort has been generated to answer this question. However, it remained a small niche for many years. It is only recently that this question has arrived at mainstream physics thanks to the topics of quantum information and computation, artificial intelligence, and quantum processes.
Last spring the Wolfram Physics Project was announced, it claimed to be a project to unify computation with physics. It is based on the ideas of Chapter 9 of NKS. It felt like a struck of fate that I’ve not only predicted the importance of these ideas but that my efforts were being pursued along by a series of very talented people and that the ideas were being developed much further. Initially, I explored the ideas of the project by myself producing a video and a popular article(to be published). In the video, I explained the fundamental component causal graphs or directed acyclic graphs play in the description of special relativity. Later I decided to get closer to the project and I attended the 2021 Wolfram Winter School of Fundamental Physics and published a small essay on discrete geometry and crystals modeling, Defect movement in lattice rewriting systems.
Currently, I’m contributing as a research affiliate to the Project. Although I was initially attracted to the relation of computation and fundamental physics, my main interests have since shifted because the tools developed in this project appear to have direct applicability to different areas of knowledge. Surprisingly the tools of the project allow us to describe the process of doing mathematics or the process of doing engineering, thereby we can talk about empirical MetaMathematics and empirical MetaEngineering.
The Empirical theory of Metamathematics
I’ve always had a soft spot for the foundation of mathematics. It may be because I had amazing math professors in my undergraduate degree. But perhaps it’s because my alma-mater hosted two world-class researchers in mathematical logic: Andrés Villaveces and Fernando Zalamea. They clearly influenced my thinking and very early on I got exposed to cutting-edge concepts like algebraic geometry and Homotopy Type Theory(I attended a course about these in 2017 by Princeton Professor Dimitris Tsementzis).
The influence of these two professors and my early exposure to contemporary mathematics allowed me to somehow miss the analytic philosophy of mathematics. This view, dominant in the 20th century claimed basically that all that matters in mathematics are the axiom system and the elaborate application of logic from these axioms. This is very contrary to a synthetic philosophy that claims that the process of doing mathematics is also fundamental to mathematics itself. This is a usual dichotomy in mathematics, usually referred to as set theory vs category theory or more conceptually as rigor vs intuition or static vs dynamic or geometric vs algebraic.
The view of contemporary mathematics is very synthetic, very much due to the influence of category theory and algebraic geometry in the current areas of mathematics. I was therefore very surprised when several works appeared last year confirming this synthetic view of mathematics in an empirical way. Moreover, one work used several tools and the framework from the physics project to analyze the process of doing mathematics by analyzing empirical data coming from theorem provers and books digitalization.
By reading these works I realized that Brian Arthur’s comment was actually correct! In these analyses, it is shown that we pack mathematics in theorems or lemmas and we use those theorems to build more complicated theorems. This is precisely what Brian’s comment was all about!! So that got me thinking if we can do this with mathematics, why not do it with technology? This was in fact Brian’s main point. Mathematics is just one technology. I had three pieces of the puzzle, the combinatorial framework for technology, the instance of mathematics in this framework, and the tools provided by the physics project to make sense of this data.
I thought several days about how could we get some empirical data from actual technologies in the real world. I have to admit that my main motivation for this process was not to understand the process of creating technologies, but rather I wanted to understand what money really is(back to economics). I figured money is just another technology, therefore if we get to the basics elements of technology, maybe we can understand why money has some of the properties it has. I actually wrote two articles, the first at the beginning of April( it has some very embryonic ideas of this project, some are correct, some are wrong, some are unexplored). The second was written just before this announcement(Ideas are much more clear in this one).
However there was one piece still missing, I couldn’t find a system I could study where I could test these ideas. I considered patents or exports(as economists usually do), design textbooks, circuit drawing software. Until finally the idea struck me.
The Game of Life(GoL) cellular automata
I must admit that although I had plenty of exposure to cellular automation in my undergraduate years. I never really considered the Gamel of Life(GoL) cellular automation particularly interesting. Although I was well aware of its properties of universality and its very “lifelike” behavior, I thought it was not a serious scientific activity(the cellular automata literally has ≪game≫ on the name). Having said this, I think there were two key reasons that explain why I ignored this system at the beginning.
I’ve always been very skeptical of toy models in science, especially complex systems. It may be my utilitarian mindset, but sometimes these models seem to be mere analogies of natural phenomena. They can be sometimes effectively used for explanatory aspects or to show a qualitative part of a phenomenon. However, they seem to be incapable of taking into account all the details of the real world and encoding that to the model.
The second reason I think mimics the realization of the book nature of the technology of Brian Arthur, on why people don’t really consider why they develop or design technology in the way they do. They just do it, it’s like a fish in an ocean. Moreover, when you explain the principles of technology to them, it sounds obvious, since you know it intuitively. However just like Brian Arthur said, it’s crucial. In this respect, I think I saw the remarkable things people engineer in the Game of life and it wasn’t surprising at all. I’ve seen things like that in other games, and even in real life. However, hidden in plain sight was the piece that I was looking for all along.
The first reason might sound paradoxical since I work with Stephen Wolfram, who has advocated the motto: “very simple rules produce highly complex behavior”. Don’t get me wrong, I clearly understand the scientific value of realizing that simple 1-dimensional cellular automata whose rules are chosen at random will have a finite not-so-small probability of being a full computer. This is not at all minor, this means in some sense that computation is not something special, it can be found all over the place(digital and physical world), even if we have a system with very simple rules. This naturally yields to wolfram’s principle of computational equivalence:
There are various ways to state the Principle of Computational Equivalence, but probably the most general is just to say that almost all processes that are not obviously simple can be viewed as computations of equivalent sophistication. — Wolfram NKS: 716–717
This principle has caused a lot of debate in the scientific community. People usually interpret it as the physical Church-Turing thesis. But there is really more to it, it is also saying that computation universality is everywhere. Whenever you find a process that is not obviously simple, you might suspect it is capable of universal computation, not more(hypercomputation), not less(Turing degrees below the Halting problem).
For me, the principle of computational equivalence is only non-vacuous if you can explicitly construct an encoding of the system. Very similar to the analytic and synthetic dichotomy in mathematics. This principle is as vacuous as the statement: “mathematics can be reduced to set theory”. But the lessons of the second part of 20th-century mathematics were not of reduction, they were of construction.
“As Grothendiek taght us, objets aren’t of great importance, it is [the relations between them] that are” — See page 335 in: J-P. Serre, Motifs, Journ. arithm. Luminy 1989 (Ed. G. Lachaud). Asterisque 198–200, Soc. Math. France, 1991, pp. 333–349.
It is then how objects relate, and how they are transformed or combined that are the lessons of 20th-century mathematics. In a sense, this is the challenge to 21st-century science,
So the history of science is the history of reduction. To understand is to take something apart and look at its constituents, so when we’re kids, someone gives us a radio or a car and we just take it apart. And there is some insight to be had by looking at what makes something up, but the harder problem is to put it together again, right? And that’s emergence, right? That’s the other side. That’s the construction side of science. The history of science is reduction, the future of science is emergence. -D. Krakauer, Santa Fe. 2019
(Update 07-08-2021 :: A very straight forward to see this challenge is as follows: Science has traditionally dealt with objects and their properties, like an electron and its charge. However, measurement is the interaction between two objects. There are several things to note in this statement, first I want you to forget about quantum mechanics and the measurement problem. What I want you to think is that a measurement is done by a device and if you think about it, Galileo first constructed the telescope, and then he did his science. So In some sense engineering is prior to science, and what we look for now it is the science of the instrument, the science of engineering - MetaEngineering)
How can we interpret this statement? I believe there are two sides to this statement. We have to understand how we humans assemble machines and how nature assembles theirs. This is another dichotomy, engineered vs evolved, controllable vs rewardable. In the first case, I believe you don’t need an agent doing the engineering. The fundamental component here is the specific way we humans assemble our machines, then this implies it is really all about sequentiality, combinatorial evolution, and an analysis of how processes compose. On the other hand, nature assemblage is not necessarily synchronous, it depends highly on competition and in error-correction pieces.
More specifically the case of nature assemblage is less understood, many pieces are fundamental, for example, many aspects of the organism we have today are contingent on some historical factors that we cannot predict. Other notions like the organisms we have today highly dependant on their development or the implicit information that the environment provides in biological processes or even more standard like natural selection or genetics. All of this seems quite different from human engineering or human science, nevertheless, I believe that that computer science and biology are not really different fields, I think we are all studying computation just in different media, and I do think there’s a lot of opportunity for back and forth.
For example, I think Wolfram’s original ideas on cellular automation are better suited to be an explanation of the contingent history of biological systems and the idea of natural selection. To the contingent part, there is this idea of computational irreducibility also known as unpredictability, where one is not capable to predict what would be the future state of a system. So to some approximation the history matters, that is I cannot expect to reduce the future outcome of the system to a short explanation given the initial conditions. The idea of selection is surprisingly captured by these systems too, it just so happens that when you have a cellular automaton capable of universal computation, there is a strange phenomenon — — sub-parts of it are always in competition with itself. So, systems which have this universal computation property are to some extent alive in the Darwin sense.
From these ideas also follows that life can emerge naturally as soon as a system that can store large amounts of information spontaneously has interactions that are capable of forming a computer. Although this is completely remarkable, this is not the full story, why? Because the life we have on earth has some regularities at all levels, at the biochemical level, at the cellular level, at the ecosystem level, etc. Where do all these regularities come from? Well, from one way is that the ingredients from which life is composed do matter, so there are constraints to the things you can actually build, even if they can perform arbitrary computations. I think this was the main weakness of Wolfram’s book, he modeled systems where irreducibility was ubiquitous. So this led him to believe that you could not predict anything in these systems, that the only way to explore them was to execute them step by step.
This last claim is absolutely correct, however, what Wolfram failed to see is that structures can be formed in these unpredictable environments, even if they have to be built step by step. Then it is the progressive understanding of each layer of complexity the thing humans have done in these environments. Biology and mathematics are the two fundamental examples. First, even if the biosphere is computationally universal, we humans have been able to progressively understand a lot of phenomena that happen in our environment, consequently, we now have a pool of empirical knowledge and a pool of regularities about our human experience with the biosphere. Similarly, in mathematics, we can start from the axioms and build the mathematical structures that are of interest to us, even if they have to be constructed step by step. Although historically, mathematics has been worked in both a high-level language, by trying to understand geometry, topology, etc. It is the same process we have been building structures of interest for us step by step, and now we have a pool of theorems and a pool of regularities of our practice of mathematics.
This missing part led Wolfram to claim that people would need to use the empirical study of simple programs to move science forward. However, this never happened… We still use mathematical equations, and except for a few areas, we use mostly complex programs in the development of science. Part of the reason, as I mentioned above is because these simple programs, although they can produce complexity, on their own, they are mainly used for qualitative and explanatory aspects and they seem to lack the ability to encode the details of the real world to the model. Now Wolfram has shifted his claims over the years to a shift from mathematical equations to computer programs. However, this is not nearly a change of scientific paradigm.
I believe the real question is which of these systems is rich enough for us humans to mine and build progressive layers of complexity such that we accumulate a pool of useful and interesting empirical knowledge and recognize a pool of regularities. I think a good example comes in the field of Artificial Intelligence. Before the deep learning revolution, people used very simple programs based on symbols, or based on real numbers(e.g., neural nets). However, at the beginning of the field, both of these techniques failed to match the expectations of researchers. Even though a single-layer neural network(with infinite width…) is capable of universal computation, single-layer neural nets are almost useless in applications. It was only years later until we humans could find a model(multi-layer Neural Nets) where the model is rich enough is expressive enough for us to explore a bunch of interesting applications(audio, image, speech, and language). We have progressively built more and more understanding and empirical knowledge on this vastly large space of architectures. Sadly, this has not happened with symbolic systems, and the field is death.
Very interestingly in this respect, the Game of Life is at a weird grey line between toy models and people progressively building structures in this unpredictable environment. There is something in this game that has captured the imagination of young coders. It not only is a visual language but it also produces beautiful and complex patterns. This naturally leads to the second point I mention above. All these structures progressively explored and built by people in the Game of Life seemed like a natural exploration of the human mind in this hostile environment, and this is precisely the point. It is difficult to step out and look at this process from afar, it is the built-in way in which we explore difficult environments. However, when I realized that this well-controlled environment provided laboratory-like conditions for studying the process in which we develop machines, I knew I’ve found the piece missing to study the power of human construction habilities.
Interestingly enough, I’m not the first one to recognize this:
“I’ve wondered for decades what one could learn from all that Life hacking. I recently realized it’s a great place to try to develop “meta-engineering” — to see if there are general principles that govern the advance of engineering and help us predict the overall future trajectory of technology. One can look at microprocessors or airplanes, but they involve all sorts of details of physics and materials. In Life there’s 50 years of “engineering development,” just applied to configurations of bits. It’s the purest example I know of the dynamics of collective human innovation.” Stephen Wolfram — NY Times
So did Stephen suspected the piece missing in his Principle of Computational Equivalence. I don’t know, but I do strongly suspect it is the case. Funny enough, I read this article in December 2020. However, nothing really stood out to me. So it was stored very deep in my subconscious. Remarkably Stephen never mentioned this topic in the time I interacted with him from December 2020 to April 2021. So perhaps the discovery on the importance of the Game of Life to develop a theory of technology was independent, it is for you to judge.
The Key Insight
So on April 12th, 2021, it finally struck me!! The Game of Life cellular automation is the perfect place to develop the theory of the process of doing engineering. You can analyze everything: the architecture, the principles, the components, the dependency tree. Everything* is there in a sequence of bits. After looking at the relevant literature on this I realized that absolutely nothing like these had been done before. The closest thing has been doing this analysis for mathematics. After looking at this amazing opportunity on the horizon I decided to quit my current line of work and dedicate my energies to this project.
*This is partially true, not everything is there. Although we have the exact geometric configuration of a particular GoL pattern. The code alone does not tell us why the pattern works at all. This explanatory information is analogous to a human proof in mathematics, you can execute the multiplication algorithm, but why does it work is a piece of extra information. The sets of reasons why a thing works are very much human, this is why sometimes machine-generated proofs are unreadable, and generally considered not satisfying. This explanatory information is a type of tacit information, and even though is generally considered irreducible(this is one of the empirical parts of mathematics or engineering, commonly known as experience). However this type of tacit knowledge I believe is to some extent reducible. Just like you learn first the grammar of a language before speaking it fluently, I believe you can learn the “grammar” of being an experienced mathematician, or the “grammar” of being an experienced engineer. These are the proper set of actions that an experienced mathematician or an experienced engineer would follow to solve a problem. But these are not abstract techniques(not at the level of mathematics or physics), these are high-level heuristics(at the level of explanation) that the experienced mathematician or engineer does to solve problems. This [topic ](https://arxiv.org/pdf/2006.02359.pdf)has also been studied recently, and some key insights are also in the theory of combinatorial evolution.
Now after two months of figuring out the details, I’ve decided to officially launch the project and keep a track of the steps I take in an online archive. In the next sections, I’ll go through the most important elements of the project and its two principal activities.
Principal Ingredients
We start by describing the most important elements in this project. Starting with the core of the project, the Game of Life, then its huge popularity, and the opportunity to study the amazing machines people have constructed over the years.
Game of Life
Let’s start from the beginning, the fundamental system that we would be analyzing is the Conway Game of Life(GoL):
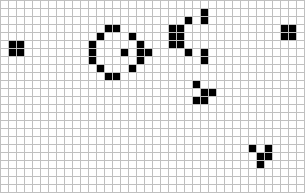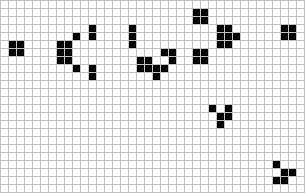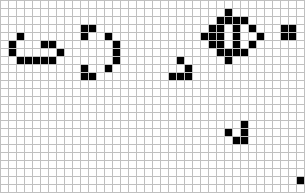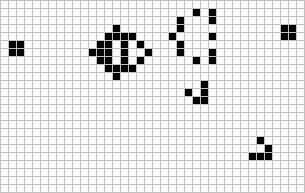 Gosper Glider Gun
Gosper Glider Gun
This is a two-dimensional cellular automaton, informally this means that we have a grid of cells, whose state can be black or white. Given an initial state, we update the state of each cell according to a local rule. For the GoL we will apply a rule at each cell, given a neighborhood region.
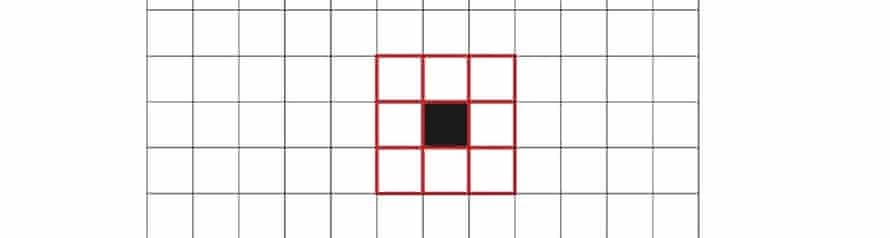 Cell Neighborhood
Cell Neighborhood
These are the rules we will consider,
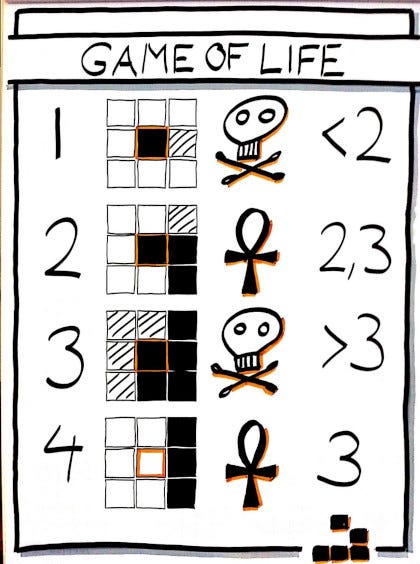
Any live cell with fewer than two live neighbors dies (referred to as underpopulation or exposure).
Any live cell with two or three live neighbors lives, unchanged, to the next generation.
Any live cell with more than three live neighbors dies (referred to as overpopulation or overcrowding).
Any dead cell with exactly three live neighbors will come to life.
Given an initial pattern, we will apply these rules to each cell and observe how the system evolves. For example, we can see what happens with these patterns as initial conditions:

As we see in this image, some patterns finish in a stable configuration, others in a gird of only white cells, and others are periodic. In general, given an initial configuration, it is impossible to know what is going to be its final state. This is known as unpredictability. This naturally leads to ou next point
Popularity
Since we are not able to predict what is going to happen with an arbitrary pattern in the GoL, people have explored empirically what are the species that live in this universe, how do they synthesize, what is their behavior, and many more things. Moreover, the game of life has maintained huge popularity in the circle of recreational mathematics and programming since its creation in the 1970s. Today there are several websites dedicated to catalog and explore all the different marvels that the game has to offer.

People have explored patterns of all sizes, cataloged them according to their global behavior, constructed machines that can be as complicated as a computer itself, and much more. An incredible piece of construction is exemplified in this digital clock:
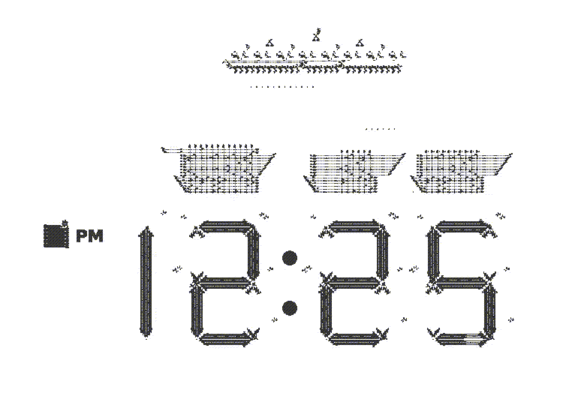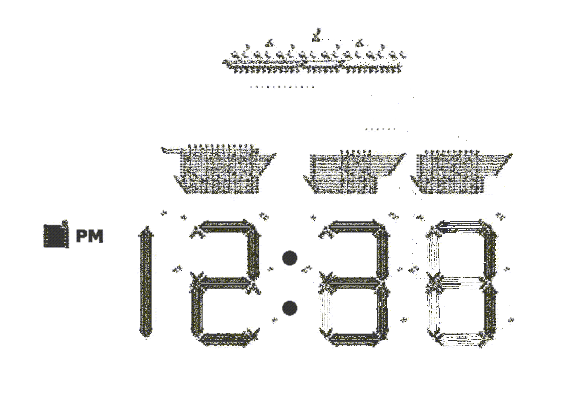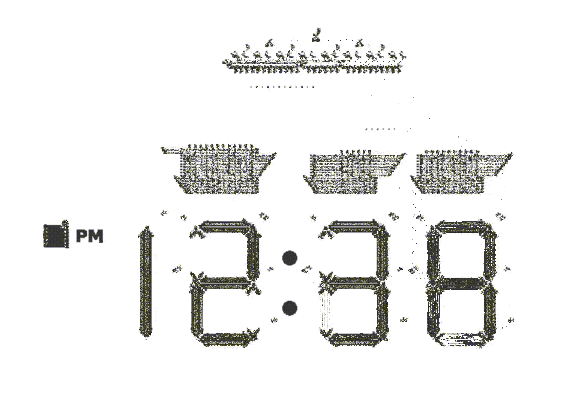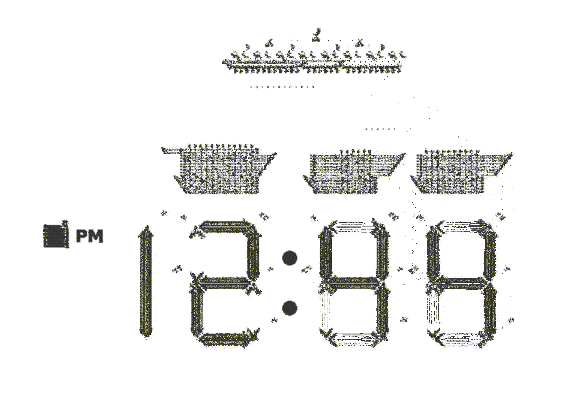
This cock requires an enormous amount of effort to construct, moreover the engineering of this clock is very finely tuned. If we change the state of a small set of cells, the pattern will not work anymore, moreover, its behavior is as we mentioned above unpredictable.
All of this sounds very cool right, but are these machines useful for some tasks, even if obscure. Well, for many years I thought there was not much to be found here. Moreover, I think that many of the Life enthusiasts didn’t really think any of their work really meant to be applied somewhere. They did it for the sake of pure human creativity and curiosity. However as I mentioned above, the following comment contains the seed of this project,
“I’ve wondered for decades what one could learn from all that Life hacking. I recently realized it’s a great place to try to develop “meta-engineering” — to see if there are general principles that govern the advance of engineering and help us predict the overall future trajectory of technology. One can look at microprocessors or airplanes, but they involve all sorts of details of physics and materials. In Life there’s 50 years of “engineering development,” just applied to configurations of bits. It’s the purest example I know of the dynamics of collective human innovation.” Stephen Wolfram — NY Times
So in all the data generated by the life enthusiast in over 50 years, we may discover very powerful principles that govern the process of doing engineering. This sounds like a great idea! But how can we do this exactly?
Combinatorial Theory of Evolution
First, we need a framework to understand the creations generated in the GoL, I claim that the theory of combinatorial evolution is a very useful way of organizing the task of constructing meta-engineering. This framework has three main principles
Principle 1:A technology is a combination of components for some purpose.
Principle 2:It follows that technology consists of building blocks that are technologies.
Principle 3:Each technology exploits an effect or phenomenon, usually several.
Using these principles we can imagine building something like a phylogenetic tree of a GoL machine. We can think of connecting technologies that have shared building blocks, and do this recursively for all the recorded machines generated in the GoL.
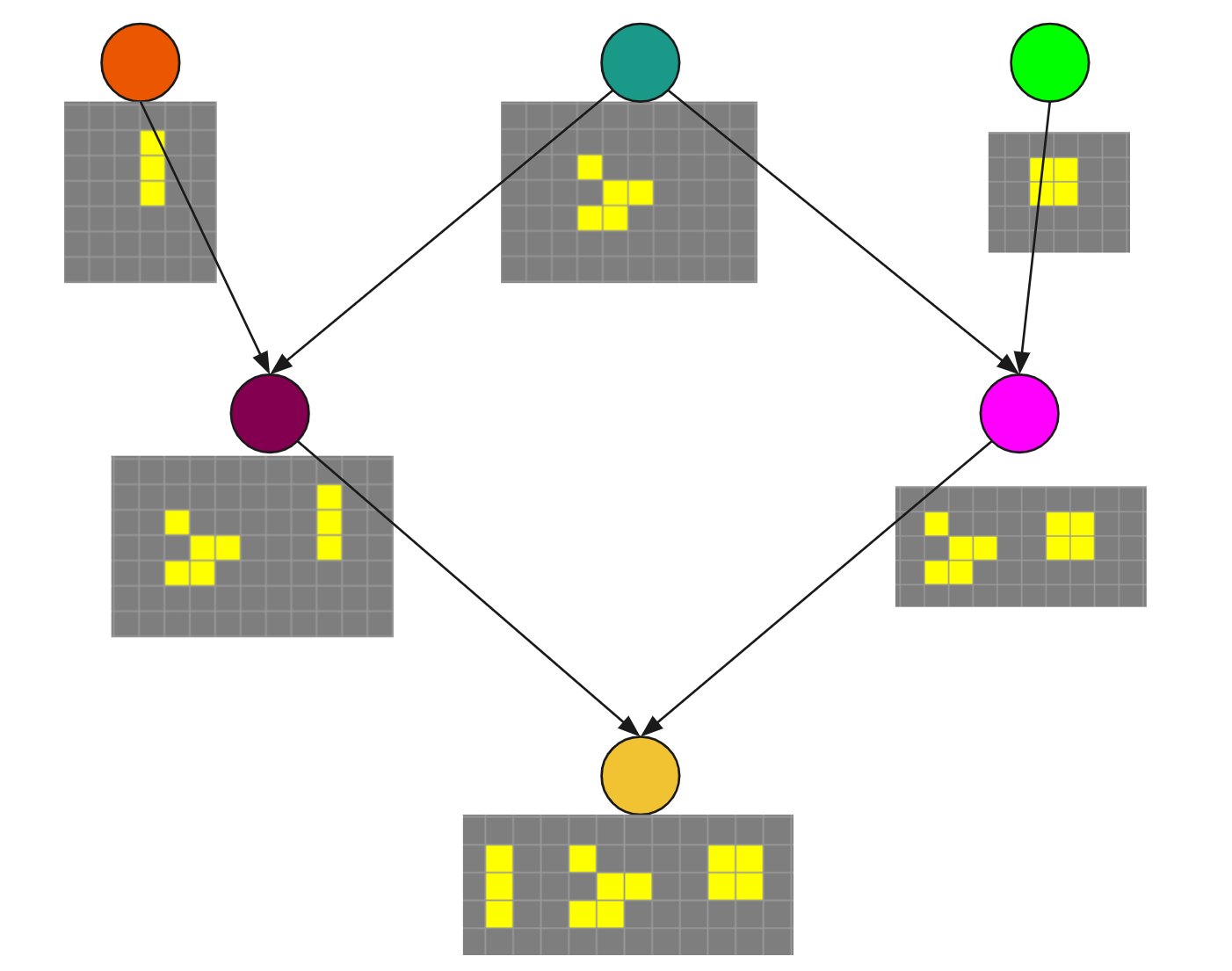
Although this sounds relatively simple, it is very non-trivial to perform this kind of classification. One needs to not only know what are the pieces that compose the piece of technology but understand the principle under which it is operating. In fact, it is really an open question if the combinatorial framework alone is enough to understand all of the patterns that we humans have constructed. I suspect that the framework is enough to understand how we humans constructed a particular machine, however, I believe that to understand the machine itself, we might need more tools. Whether this is something that blocks the generation of a phylogenetic tree is an open question, but I suspect that in order to understand self-replicating patterns we need more than just the combinatorial framework. I’ll briefly talk about this at the end of the text.
Database Construction
One of the objectives of this project is to construct a database with a large amount of GoL patterns that state explicitly what are explicitly the components used to build a particular pattern. Among the current GoL databases, there is no database that contains this information explicitly.

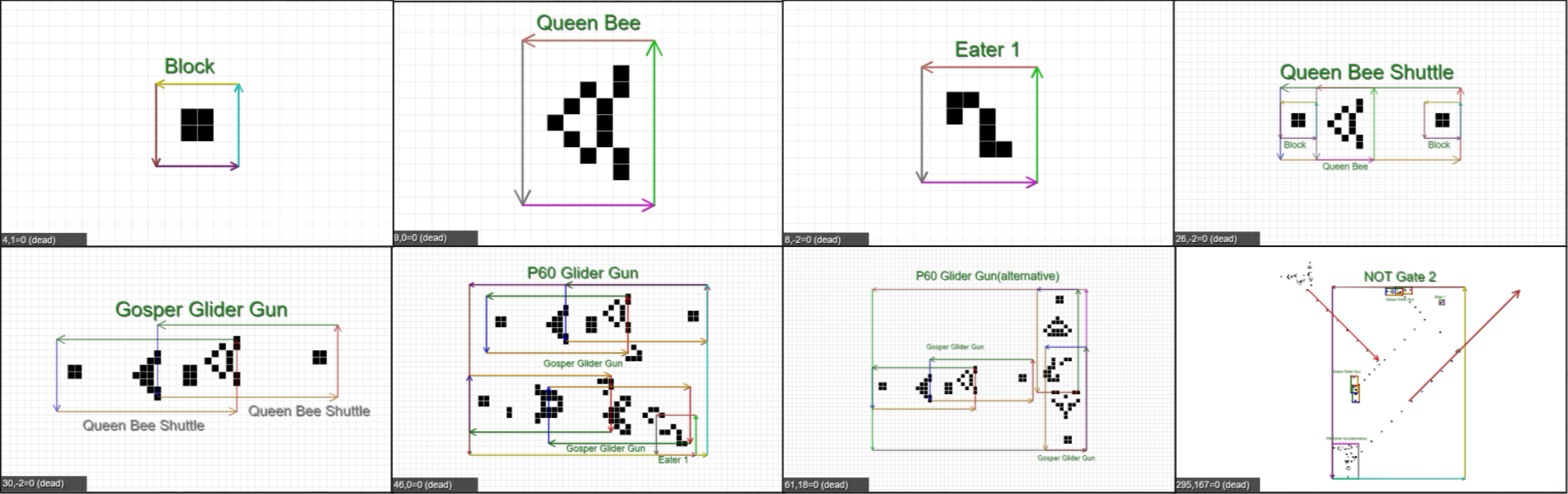
These databases contain patterns organized by some empirical properties life enthusiasts have found important over the years, for example, the Stephen A. Silver Lexicon has the following structure,
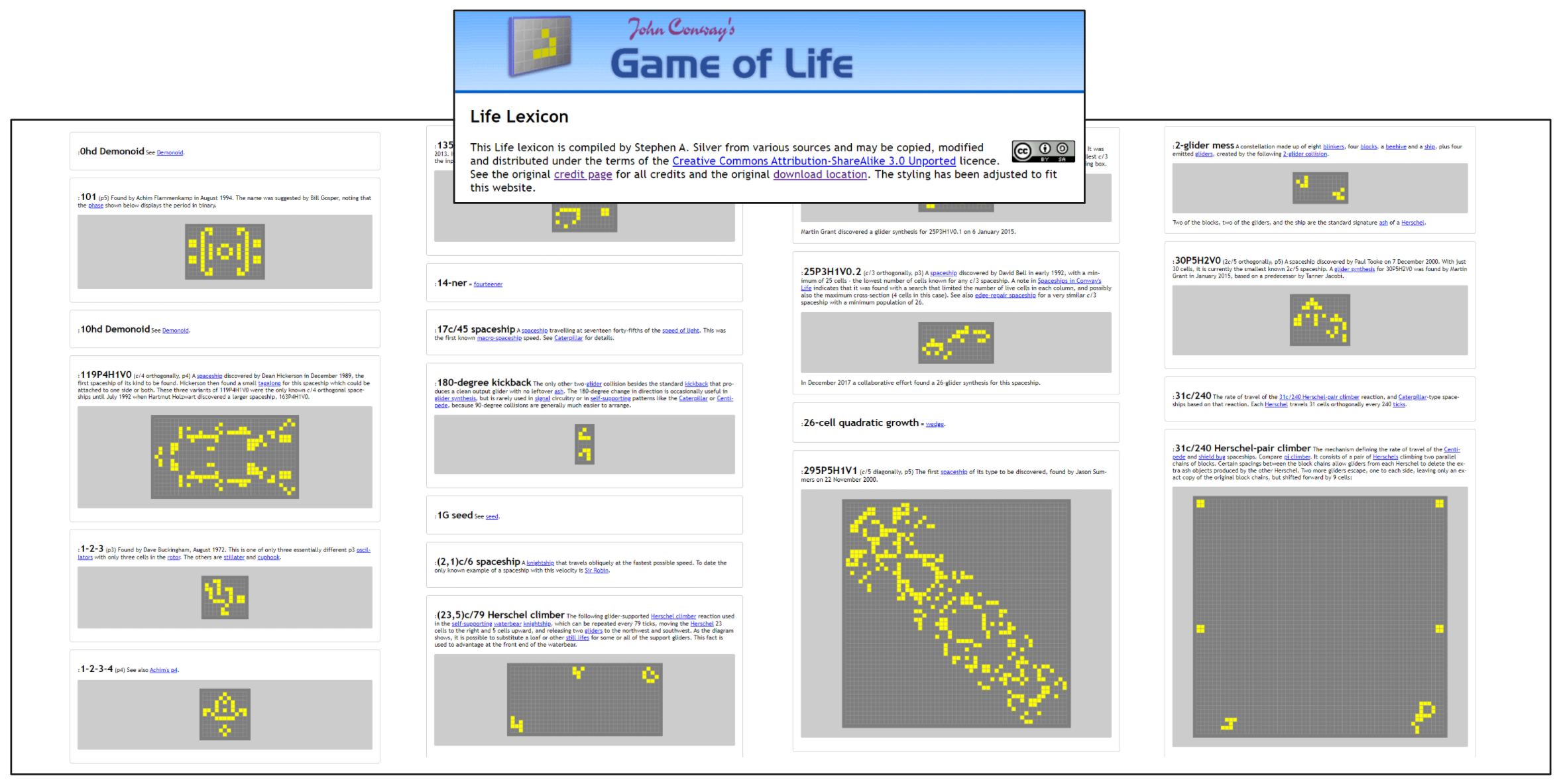
However our task is very different, we want to know if given an arbitrary pattern, does it have an internal structure ? or not? For example, consider this 2-engine Cordership, is it correct to think about it in terms of sub-pieces?
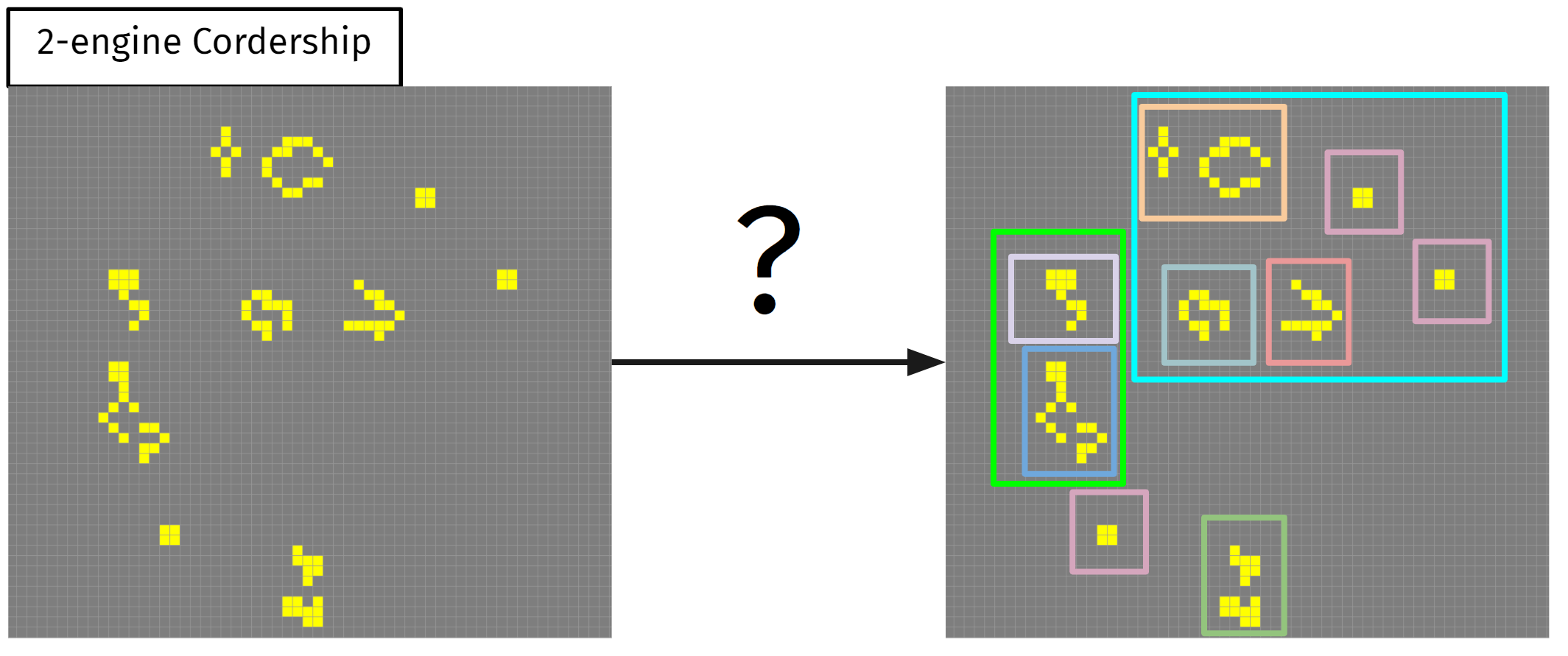
Or is it perhaps better to think about it as only one piece? This is an open question, moreover, the GoL enthusiasts don’t really think that way… This piece has discovered recently, and the current paradigm in the GoL community is all about Glider synthesis. This kind of thinking is more biological, in terms of a type of metabolism that requires only gliders. I believe that this framework has to be explored in the modern paradigm of GoL machines, this is the second part of this project(Gemini Expedition). Having said this, there are more “classical” machines in the GoL, in fact, our database has currently 8 classified patterns and 34 recognized patterns to be classified in the framework of the combinatorial framework. A snapshot is shown next,
The aim of this project is to classify a large number of patterns that have been constructed in the last 50 years and analyze some of the general properties that underlie these boosts of creativity. For example, an objective of the project is to properly classify this 8-bit computer, which is not only a universal turning machine but is a computer in its modern form.
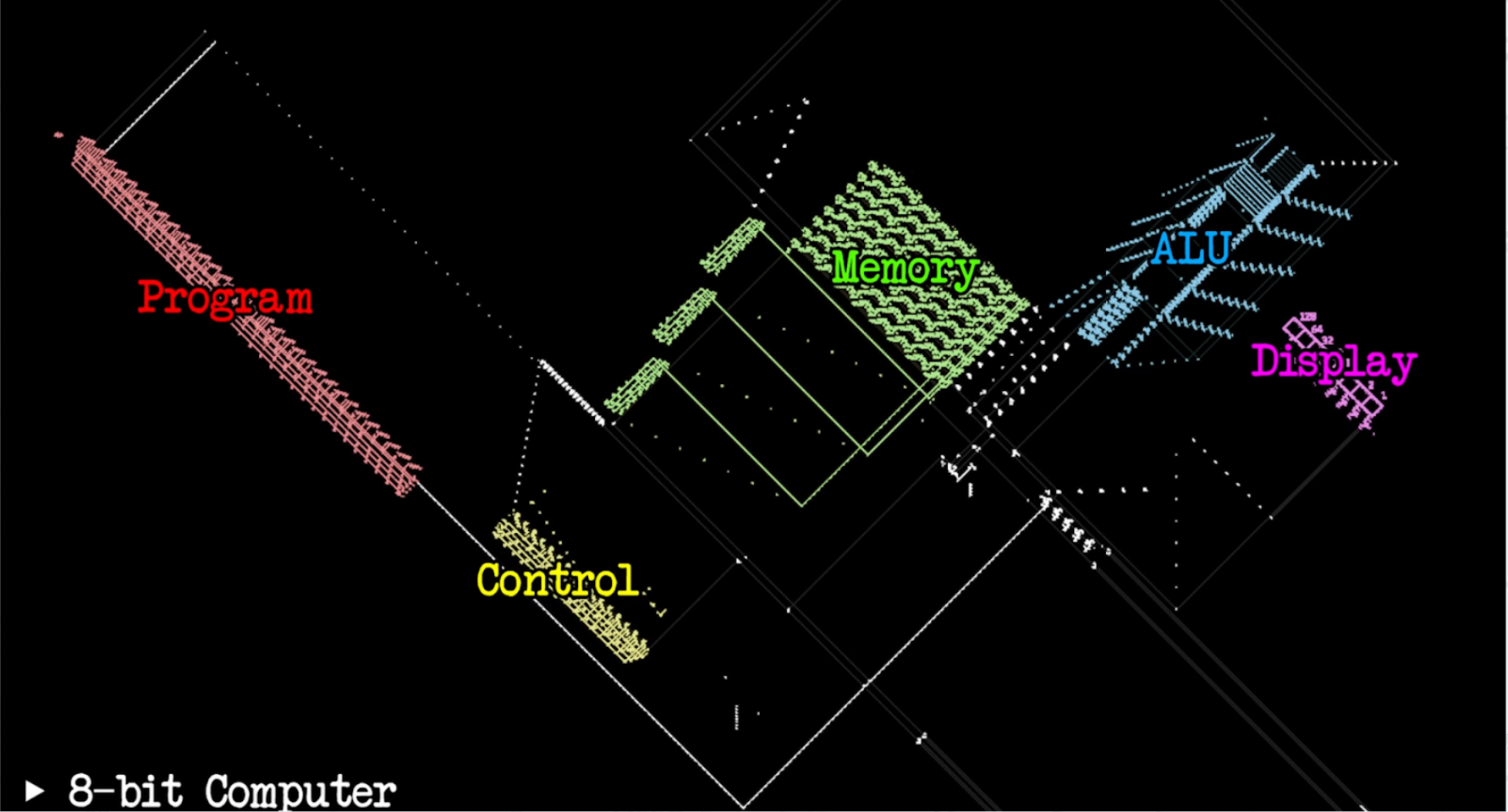 8-bit computer as shown in https://youtu.be/Kk2MH9O4pXY
8-bit computer as shown in https://youtu.be/Kk2MH9O4pXY
This and other patterns would be classified in the database.
Gemini Expedition
I must admit that my original idea was only to generate the previous database. However when I first presented my project in the seminar of the Wolfram Physics Project. I noticed something, I couldn’t get my message through, I failed as a salesman of my idea. Therefore I remembered Kevin Buzzard trying to sell his idea about a library of formal mathematics. He did two things, he formalized an incredible difficult object in mathematics and one also that was popular today among mathematicians. So that is the spirit of the Gemini Expedition, I’m going to try and understand the 0E0P Metacell.

Not only it is one of the most complicated patterns ever devised in the GoL, but it is incredibly popular among life enthusiasts today, in fact in 2018 it got second place in the pattern of the year award. Therefore this is one of the main objectives of this project the successful understanding of this pattern.
I must also say that I did not only choose this pattern because of popularity and difficulty. I believe that the understanding of this pattern is of great importance for science. This pattern is not only a self-replicating pattern but is also a universal constructor. In the study of such a pattern I believe lies the future of science and engineering. So I hope I can contribute to the overall understanding of these patterns.
So why did I call it the Gemini expedition? Because it is meant to be a sort of digital expedition to an isolated land of the internet(Conwaylife.com), where all these machines and patterns have been constructed. Then me as the “conquistador”, I’ll travel just like Darwin or Humbolt did, to try and understand what marvelous devices have these people constructed in over 50 years. Also, I called it Gemini, because I’m quite interested in the idea of self-replication and how can we humans borrow some ideas of nature and the GoL community to construct such creatures in our physical engineering world.
The expedition has its own section on the website, and I’m going to live-stream a lot of my research process, it will be recorded in the youtube account, Gálapagos Project. Also, the Twitter account Galápagos Project would be tweeting about it. So what would be more or less the timeline of the expedition? I’m planning to do it more or less the following way,
Construction of the Demonoid
Exploration of Self-Constructing Spaceships and Tools
Exploration of different Universal Constructor Patterns
Exploration of Self-Replicating patterns
Exploration of the 0E0P Metacell.
Objectives and Deliverables
Some of the objectives are to solve these open questions,
Is the combinatorial evolution framework capable of describing all these devices?
Are there events like Cambrian Explosions?
What are the differences between the individuals found in the GoL and the ones found in nature?
What can this project say about the future of technology and other areas of science and engineering?
What can novel theories like constructor theory or assembly theory say about GoL self-replicating patterns?
Is a metabolism view of patterns relevant for the synthesized patterns?
and finally, I’m planning to have the following deliverables for the project,
A main scientific article
An interactive version of the article on this website
A database of GoL patterns and their subparts
An interactive way to look at the GoL database on this website
Two introductory videos explaining the main ideas (Economics, Technology)
The Analysis of several self-replicating structures in GoL (the exact deliverable in consideration)